Sheet 4

Task 1

Give an extensive formulation of the multicommodity flow problem and show that it can be derived by Dantzig Wolfe decomposition of the previously seen (compact) arc flow formulation.

• What is the complete Master Problem?
• What is the column generation subproblem?

Task 2

Consider generalized assignment problem with equality constraints:

Solve an instance by delayed column generation treating the constraints $\sum_{j=1}^n x_{ij}= 1 \qquad i = 1,\ldots, m$ as the complicating ones and $m=3,n=2,[a_{ij}]=\begin{bmatrix}5&3\\3&8\\2&10\end{bmatrix},[c_{ij}]=\begin{bmatrix}20&16\\15&19\\19&14\end{bmatrix}$ and $[b_j]=\begin{bmatrix}6\\21\end{bmatrix}$.

Task 3

You are the person in charge of packing in a large company. Your job is to skillfully pack items of various weights in a box with a predetermined capacity; your aim is to use as few boxes as possible. Each of the items has a known weight and the upper limit of the contents that can be packed in a box is 9 kg. There is no concern with the volume they occupy. So, how should these items be packed?

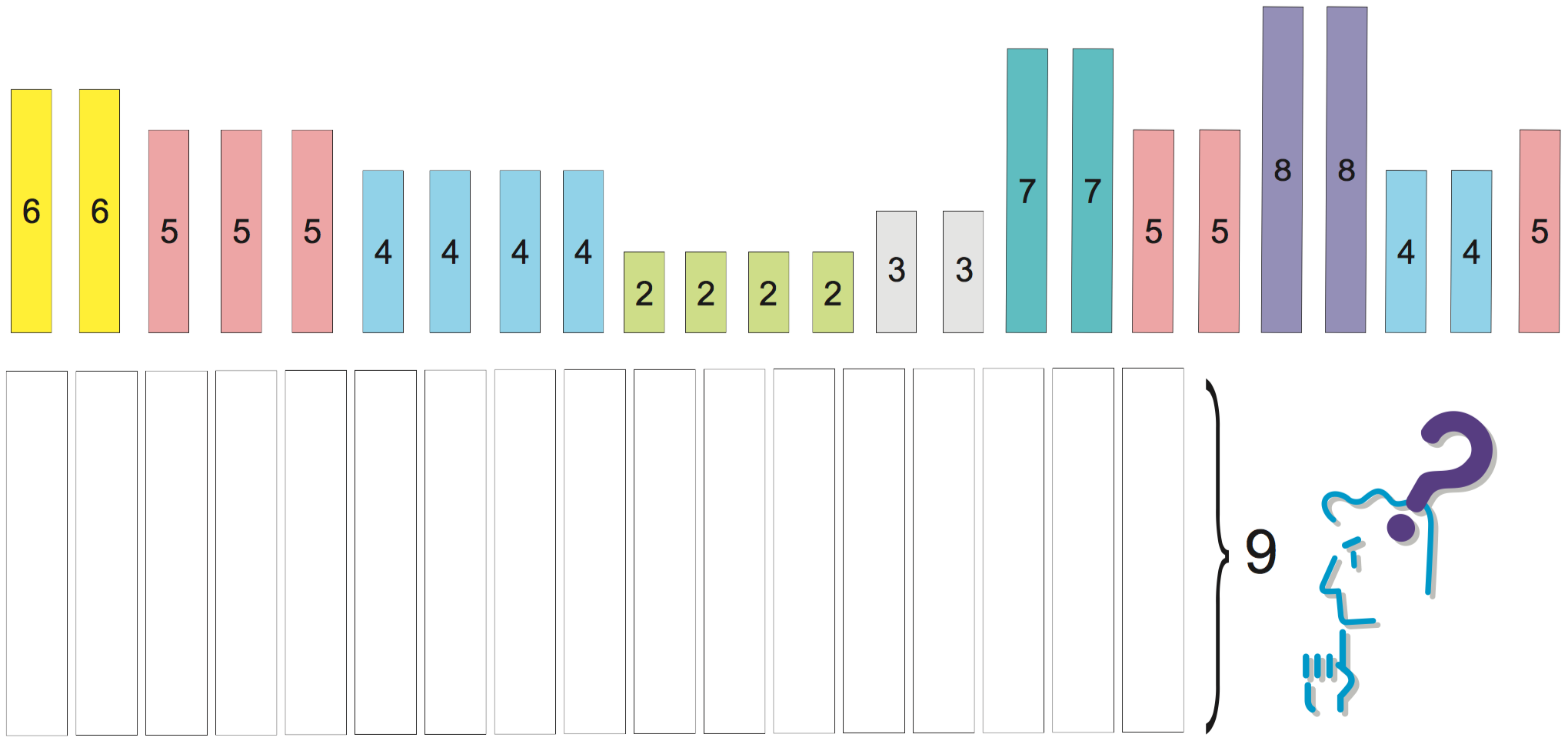
This is an example of a problem called the bin packing problem. It can be described mathematically as follows.

Bin packing problem

There are $n$ items to be packed and an infinite number of available bins of size $B$. The sizes $0\leq s_i \leq B$ of individual items are assumed to be known. The problem is to determine how to pack these $n$ items in bins of size $B$ so that the number of required bins is minimum.

1. Formulate the problem using a compact formulation and an extensive formulation.

2. Solve the given example using the extensive formulation. Solve the linear relaxation of the master problem by column generation and draw a plot about the dual bound development during the process.

3. Continue the process with branch and price if the solution found at the previous point is not integral.

def BinPackingExample():
    B = 9
    s = [6, 6, 5, 5, 5, 4, 4, 4, 4, 2, 2, 2, 2, 3, 3, 7, 7, 5, 5, 8, 8, 4, 4, 5]
    return s,B


def FFD(s, B):
    remain = [B]
    sol = [[]]
    for item in sorted(s, reverse=True):
        for j,free in enumerate(remain):
            if free >= item:
                remain[j] -= item
                sol[j].append(item)
                break
        else:
            sol.append([item])
            remain.append(B-item)
    return sol

You find these data and some starting templates for your implementations in Python in our git repository [GIT]:

• A template for the compact formulation: compact_template.py.

• A template for the extended formulation with delayed column generation: extensive_template.py

To add columns to your model without resolving from scratch see:

• In gurobipy, the last example from this doumentation page: Modify a model (gurobi.com)

• In Python MIP see documentation for Column and add_var.

• In Pyomo see cutting_stock.py

• In Pyscipopt there is a different philosophy. See test_pricer.py. Alternatively it is possible to follow this example.