DM872 (S24)

Mathematical Optimization at Work

Sheet 4

Task 1

Give an extensive formulation of the multicommodity flow problem and show that it can be derived by Dantzig Wolfe decomposition of the previously seen (compact) arc flow formulation.

Solution:
Handwritten notes taken from reference [AMO].

Task 2

Consider generalized assignment problem with equality constraints:

\[\begin{align} \max &\sum_{i=1}^m\sum_{j=1}^n c_{ij}x_{ij}\\ &\sum_{j=1}^n x_{ij}= 1 \qquad i = 1,\ldots, m\\ &\sum_{i=1}^m a_{ij} x_{ij}\leq b_j \qquad j = 1,\ldots,n\\ &x \in \{0, 1\}^{mn}. \end{align}\]

Solve an instance by delayed column generation treating the constraints $\sum_{j=1}^n x_{ij}= 1 \qquad i = 1,\ldots, m$ as the complicating ones and $m=3,n=2,[a_{ij}]=\begin{bmatrix}5&3\\3&8\\2&10\end{bmatrix},[c_{ij}]=\begin{bmatrix}20&16\\15&19\\19&14\end{bmatrix}$ and $[b_j]=\begin{bmatrix}6\\21\end{bmatrix}$.

Solution:
This is an example of unrelated parallel machine scheduling problem, where machines are indexed by $j$ and jobs (activities, tasks) by $i$. We can apply Dantzig-Wolfe decomposition to GAP treating the assignment constraints as the linking and complicating constraints defining the master problem and the machine capacity constraints as the block constraints defining the subproblems. Let $K_j$ be the number of solutions to the knapsack subproblem: $$ \begin{align} &\sum_{1\leq i\leq m}w_{ij}y^j_i\leq d_j\\ &y^j_i\in \{0,1\}, \quad i=1,\ldots,m \end{align} $$ Any solution to this problem, indexed by $k=1,\ldots,K_j$, i.e. $\vec y^j_k=(y^j_{1k},y^j_{2k},\ldots,y^j_{mk})$, represents a feasible assignment of tasks to a machine $j$. The master problem becomes: $$ \begin{align} z_{RLMP}=\max &\sum_{1\leq j\leq n}\sum_{1\leq k\leq K_j}\left(\sum_{1\leq i\leq m} p_{ij}y^j_{ik}\right)\lambda_k^j\\ \label{alphas}&\sum_{1\leq j\leq n}\sum_{1\leq k\leq K_j}y^j_{ik}\lambda_k^j=1,\qquad i=1,\ldots,m\\ \label{betas}&\sum_{1\leq k\leq K_j}\lambda_k^j=1,\qquad j=1,\ldots,n\\ &\lambda_k^j\in \{0,1\}, \qquad j=1,\ldots,nk=1,\ldots,k \end{align} $$ To solve the problem by branch and bound we need to find the solutions of the linear relaxation. Let LMP be the linear relaxation of the problem. Since we have exponentially many variables, we solve the problem by (delayed) column generation. Let RLMP be the problem restricted to a subset of variables and let $\alpha_i$ and $\beta_j$ be the dual variables associated with constraint \eqref{alphas} and \eqref{betas}, respectively. The pricing (reduced cost) of a variable is given by: $$ \overline{c}_{j}=\sum_{i=1}^mp_{ij}y_{i}^j-\sum_{i=1}^m\alpha_iy^j_{i}-\beta_j. $$ In the pricing problems (one for each machine $j$) we maximize $\overline{c}_{j}$ looking for columns with positive reduced cost. Note that for a given machine $j$, $\beta_j$ is fixed and can be removed from the objective function of the pricing problem. Hence, the subproblems become: $$ \begin{align} z^j_{PP}=\max&\sum_{i=1}^mp_{ij}y_{i}^j-\sum_{i=1}^m\alpha_iy^j_{i}\\ &\sum_{1\leq i\leq m}w_{ij}y^j_i\leq d_j\\ &y^j_i\in \{0,1\}, \quad i=1,\ldots,m \end{align} $$ If $z^j_{PP}-\beta_j>0$, then the column found must be added to the RLMP. Otherwise, if no such a column is found in none of the machines, we have solved the problem. Example taken from: - "Branch-And-Price: Column Generation For Solving Huge Integer Programs". Cynthia Barnhart, Ellis L. Johnson, George L. Nemhauser, Martin W. P. Savelsbergh, And Pamela H. Vance. OR, 1998. - ex 3 p 233 of reference [Wo].

Task 3

You are the person in charge of packing in a large company. Your job is to skillfully pack items of various weights in a box with a predetermined capacity; your aim is to use as few boxes as possible. Each of the items has a known weight and the upper limit of the contents that can be packed in a box is 9 kg. There is no concern with the volume they occupy. So, how should these items be packed?

Weights of items to be packed in bins of size 9
6, 6, 5, 5, 5, 4, 4, 4, 4, 2, 2, 2, 2, 3, 3, 7, 7, 5, 5, 8, 8, 4, 4, 5

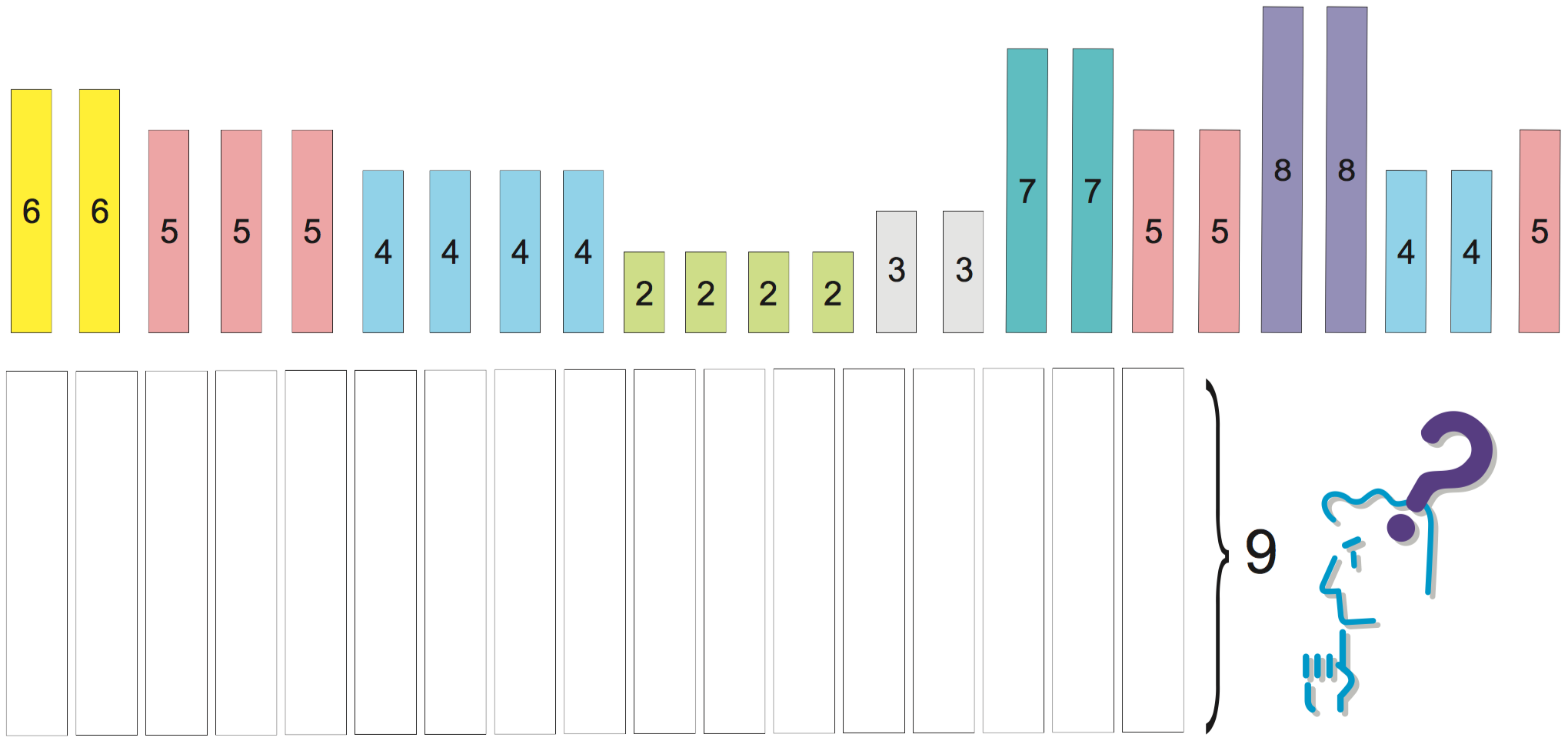
instance

This is an example of a problem called the bin packing problem. It can be described mathematically as follows.

Bin packing problem

There are $n$ items to be packed and an infinite number of available bins of size $B$. The sizes $0\leq s_i \leq B$ of individual items are assumed to be known. The problem is to determine how to pack these $n$ items in bins of size $B$ so that the number of required bins is minimum.

  1. Formulate the problem using a compact formulation and an extensive formulation.

  2. Solve the given example using the extensive formulation. Solve the linear relaxation of the master problem by column generation and draw a plot about the dual bound development during the process.

  3. Continue the process with branch and price if the solution found at the previous point is not integral.


def BinPackingExample():
    B = 9
    s = [6, 6, 5, 5, 5, 4, 4, 4, 4, 2, 2, 2, 2, 3, 3, 7, 7, 5, 5, 8, 8, 4, 4, 5]
    return s,B


def FFD(s, B):
    remain = [B]
    sol = [[]]
    for item in sorted(s, reverse=True):
        for j,free in enumerate(remain):
            if free >= item:
                remain[j] -= item
                sol[j].append(item)
                break
        else:
            sol.append([item])
            remain.append(B-item)
    return sol

You find these data and some starting templates for your implementations in Python in our git repository [GIT]:

To add columns to your model without resolving from scratch see:

Solution:
See the source code in github or this external notebook.